最终目标!!!

贝尔曼公式 Bellman Equation

定义

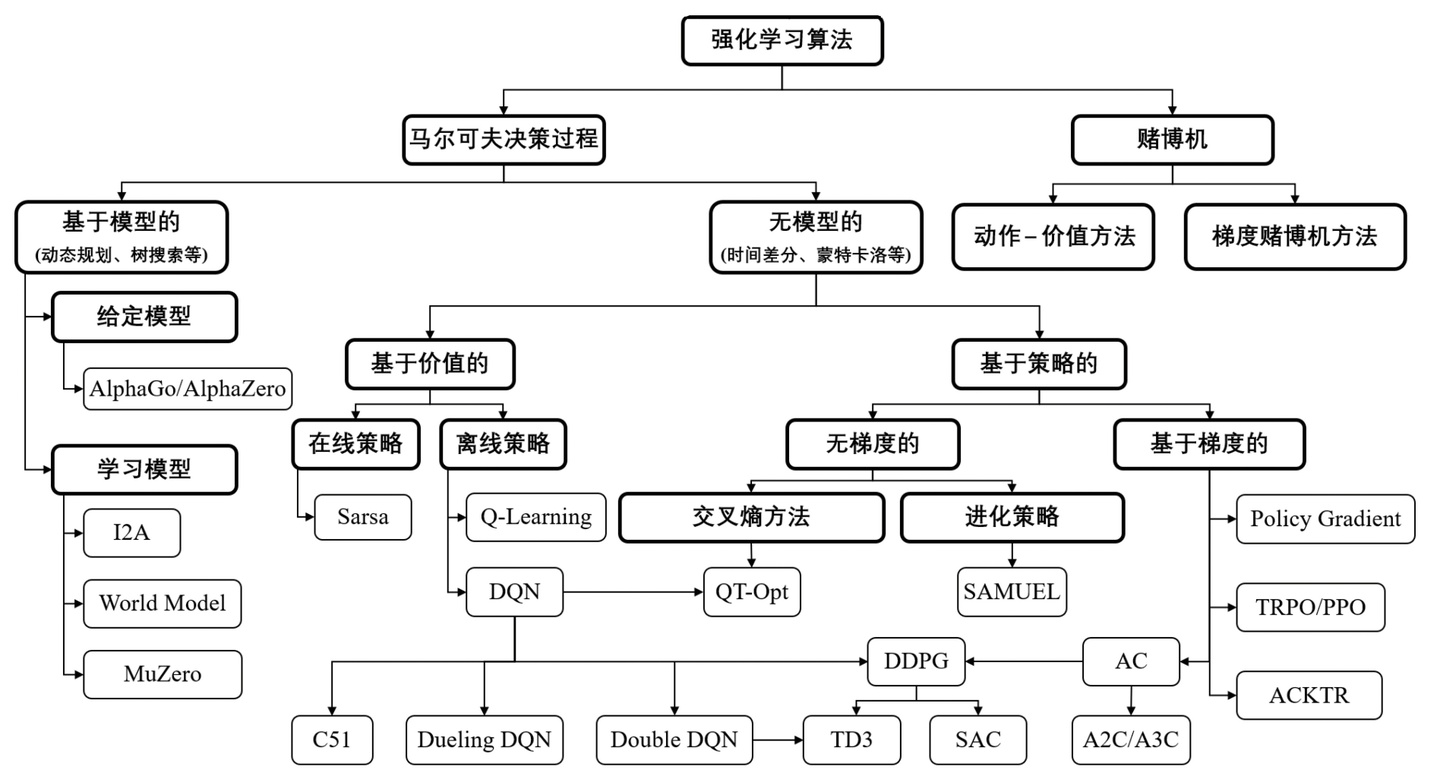
1. 回报（Return）和价值（Value）

我们定义回报 (Return) $G_t$。这是 Agent 从时刻 $t$ 开始，一直持续到未来所能获得的折扣累计奖励：

$$G_t=R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+\dots$$

• $R_{t+1}$：执行动作后的即时奖励（reward）。
• $\gamma \in [0,1]$：折扣因子（Discount Factor）。
• 注：奖励（reward）是即时的，回报（return）是累计的。

这里面可以用递归的技巧写出：

$$G_t=R_{t+1}+\gamma G_{t+1}$$

---

2. 状态价值函数（State Value）

状态价值函数 $v_{\pi }(s)$ 定义为：在状态 $s$ 下，遵循策略 $\pi$ 能获得期望回报（average return）。

$$v_{\pi }(s)={\mathbb{E}}_{\pi }[G_t|S_t=s]$$

• 这里是回报（全局概念）而不是奖励（reward）

---

3. 动作价值函数（Action Value）

在状态 $s$ 下，遵循策略 $\pi$ 采取动作 $a$，能获得期望回报（average return）。

$$q_{\pi }(s,a)={\mathbb{E}}_{\pi }[G_t|S_t=s,A_t=a]$$

• 和 State Value 的差异就是它选择了一个 action

因此：

$$v_{\pi }(s)=\sum _a\pi (a|s)q_{\pi }(s,a)$$

‍

推导

基于上述定义，我们将 $G_t$ 的递归形式代入价值函数的定义，进行展开。

$$\begin{array}{rl}{v}_{\pi }(s)& ={\mathbb{E}}_{\pi }[G_t|S_t=s]\\ & ={\mathbb{E}}_{\pi }[R_{t+1}+\gamma G_{t+1}|S_t=s]\text{(代入递归定义)}\\ & ={\mathbb{E}}_{\pi }[R_{t+1}|S_t=s]+\gamma {\mathbb{E}}_{\pi }[G_{t+1}|S_t=s]\end{array}$$

这里分出来两个期望，分别是下一步的即时 reward 和未来的 return

1. ${\mathbb{E}}_{\pi }[R_{t+1}|S_t=s]$：

$$\begin{array}{rl}\mathbb{E}[R_{t+1}|S_t=s]& =\sum _a\pi (a|s)\underset{\text{选定动作 a 后的期望奖励}}{\underbrace{\mathbb{E}[R_{t+1}|S_t=s,A_t=a]}}\\ & =\sum _a\pi (a|s)[\sum _{r}p(r|s,a)r]\end{array}$$

• 第一步：由于 $\pi$ 是个策略函数，输出多个动作，而每个动作都是一个可能性，因此 $E_{\pi }$ 需要拆成对每个动作进行求和，$\pi (a|s)$ 是在状态 $s$ 下，选择动作 $a$ 的概率

• 第二步：$\sum _{r}p(r|s,a)r$ 是一个环境反馈项

  • $r$ 是状态 $s$ 和动作 $a$ 下，环境给予的奖励（reward）
  • $p(r|s,a)$ 自不必说，是这个奖励 $r$ 的概率

‍

2. ${\mathbb{E}}_{\pi }[G_{t+1}|S_t=s]$：

这里的遍历性（期望如何展开）在于，在 $s$ 下还能去哪些状态 $s^{\prime }$，和 1 一样，我们自然而然的对下一状态 $s^{\prime }$ 进行展开：

$$\mathbb{E}[G_{t+1}|S_t=s]=\sum _{s^{\prime }}\mathbb{E}[G_{t+1}|S_t=s,S_{t+1}=s^{\prime }]p(s^{\prime }|s)$$

这里还存在期望项没有展开完，我们还需要继续进行，而由于 RL 算法一般假设马尔可夫过程，因此在求 $s^{\prime }$ 期望时，$s$ 是不必要的，因此又可写成：

$$\mathbb{E}[G_{t+1}|S_t=s]=\sum _{s^{\prime }}\mathbb{E}[G_{t+1}|S_{t+1}=s^{\prime }]p(s^{\prime }|s)$$

这里面有个容易注意到的事实（但我来说难以注意），$\mathbb{E}[G_{t+1}|S_{t+1}=s^{\prime }]$ 恰好是我们刚刚定义的 $v_{\pi }(s)={\mathbb{E}}_{\pi }[G_t|S_t=s]$，其意义是站在 $s$ 状态下的期望回报，只需换成 $s^{\prime }$，于是我们写成（又一递归形式）：

$$\mathbb{E}[G_{t+1}|S_t=s]=\sum _{s^{\prime }}{v}_{\pi }(s^{\prime })p(s^{\prime }|s)$$

但这并非我们想要的项，因为 $p(s^{\prime }|s)$ 包含 $s^{\prime }$，而对于一个站在状态 $s$ 的智能体来说，是只能通过某个动作 $a$ 转换到 $s^{\prime }$，因而我们需要把 $p(s^{\prime }|s)$ 转成如此形式：

$$p(s^{\prime }|s)=\sum _{a}p(s^{\prime }|s,a)\pi (a|s)$$

分别是状态 $s$ 下，采取动作 $a$ 能够到 $s^{\prime }$ 的概率，以及状态 $s$ 下，策略 $\pi$ 能够生成动作 $a$ 的概率，其实就是 $s$ 到 $s^{\prime }$ 的所有路径概率之和，最后代回得到：

$$\mathbb{E}[G_{t+1}|S_t=s]=\sum _{s^{\prime }}{v}_{\pi }(s^{\prime })[\sum _{a}p(s^{\prime }|s,a)\pi (a|s)]$$

‍

3. 贝尔曼方程

上面求的所有中间结果代回：

$$\begin{array}{rl}{v}_{\pi }(s)& ={\mathbb{E}}_{\pi }[R_{t+1}|S_t=s]+\gamma {\mathbb{E}}_{\pi }[G_{t+1}|S_t=s]\\ & =[\sum _a\pi (a|s)\sum _{r}p(r|s,a)r]+\gamma [\sum _{s^{\prime }}{v}_{\pi }(s^{\prime })\sum _{a}p(s^{\prime }|s,a)\pi (a|s)]\end{array}$$

我们发现里面都有 $\sum _a\pi (a|s)$，直接提出（求和）：

$$v_{\pi }(s)=\sum _a\pi (a|s)[\underset{\text{即时奖励}}{\underbrace{\sum _{r}p(r|s,a)r}}+\gamma \underset{\text{折现后的未来价值}}{\underbrace{\sum _{s^{\prime }}p(s^{\prime }|s,a)v_{\pi }(s^{\prime })}}]$$

这就是贝尔曼方程

‍

注意这是个递推式，只描述了状态 $s$ 下如何求价值函数，要求解需要对每个状态列出方程组成方程组求解。

‍

‍

其次，把 $\sum _a\pi (a|s)$ 提出写成这样的形式是有一定的妙处的，可以发现 $\sum _a\pi (a|s)$ 是一个策略，而方括号里面都是价值，包括了即时和未来两项，我们回到动作价值的定义，后面就是 Action Value：

$$q_{\pi }(s,a)=\sum _{r}p(r|s,a)r+\gamma \sum _{s^{\prime }}p(s^{\prime }|s,a)v_{\pi }(s^{\prime })$$

‍

矩阵表示

由于我们上面求出的是个递推式，为了全局求解，我们实际上需要列出方程组，因此先推导矩阵表示，我们回到提出 $\pi (a|s)$ 之前，引入记号代表两项

1. 即时奖励部分

$$R_{\pi }(s)\triangleq \sum _a\pi (a|s)\sum _{r}p(r|s,a)r$$

2. 未来回报部分

$$P_{\pi }(s^{\prime }|s)\triangleq \sum _a\pi (a|s)p(s^{\prime }|s,a)$$

有了这两个记号原来的方程可以简化为：

$$v_{\pi }(s)=R_{\pi }(s)+\gamma \sum _{s^{\prime }}{P}_{\pi }(s^{\prime }|s)v_{\pi }(s^{\prime })$$

再写成向量表示：

• 价值向量 ${\mathbf{v}}_{\pi }$ ($N\times 1$)：$[v_{\pi }(s_1),v_{\pi }(s_2),\dots ,v_{\pi }(s_N){]}^T$
• 奖励向量 ${\mathbf{R}}_{\pi }$ ($N\times 1$)：$[R_{\pi }(s_1),R_{\pi }(s_2),\dots ,R_{\pi }(s_N){]}^T$
• 转移矩阵 ${\mathbf{P}}_{\pi }$ ($N\times N$)：第 $i$ 行第 $j$ 列的元素 $[P{]}_{\pi ,ij}=P_{\pi }(s_j|s_i)$

于是直接写成：

$${\mathbf{v}}_{\pi }={\mathbf{R}}_{\pi }+\gamma {\mathbf{P}}_{\pi }{\mathbf{v}}_{\pi }$$

由于 ${\mathbf{R}}_{\pi }$ 和 ${\mathbf{P}}_{\pi }$ 都是已知的（假设我们知道环境），上面又是线性方程组，可以直接推导解析解：

$$\begin{array}{rl}{\mathbf{v}}_{\pi }-\gamma {\mathbf{P}}_{\pi }{\mathbf{v}}_{\pi }& ={\mathbf{R}}_{\pi }\\ (\mathbf{I}-\gamma {\mathbf{P}}_{\pi }){\mathbf{v}}_{\pi }& ={\mathbf{R}}_{\pi }\\ {\mathbf{v}}_{\pi }& =(\mathbf{I}-\gamma {\mathbf{P}}_{\pi }{)}^{-1}{\mathbf{R}}_{\pi }\end{array}$$

但实际中解析解通常求不出来，原因如下：

1. 如果 $N$ 很大，矩阵求逆会非常困难，复杂度 $O(N^3)$，而实际问题中，$N$ 一般都很大
2. 有时我们不知道 ${\mathbf{P}}_{\pi }$ 和 ${\mathbf{R}}_{\pi }$ 是什么，或者难以模拟，被称为 Model-Free 场景

‍

于是我们需要一种迭代求解方法

‍

贝尔曼最优方程 bellman optimal equation

首先我们定义何为最优 ， 这和博弈论的优势策略是一样的：

$$v_{\pi }(s)\ge v_{{\pi }^{\prime }}(s),\mathrm{\forall }s\in S$$

我们就说策略 $\pi$ 优于或等于 ${\pi }^{\prime }$

基于此，我们要寻找的最优状态价值函数 $v_{\ast }(s)$ 定义为所有可能策略下的最大值：

$$v_{\ast }(s)=\underset{\pi }{max}{v}_{\pi }(s)$$

这就引出几个问题：

1. 这样的策略是否存在？
2. 这样的策略是否唯一？
3. 这样的策略是随机策略还是确定性策略？
4. 如何达到这样的策略？

‍

我们继续用上面矩阵表示的记号，对于任意固定策略 $\pi$，价值函数满足线性方程：

$$v_{\pi }=r_{\pi }+\gamma P_{\pi }{v}_{\pi }$$

观察上式，实际上的未知变量只有 $v_{\pi }$，我们可以看作是：

$$v=f(v)$$

其中：

$$f(v):=\underset{\pi }{max}(r_{\pi }+\gamma P_{\pi }v)$$

这个形式可以用不动点定理，需证明 $f(v)$ 是个收缩映射：

对于任意两个价值向量 $u$ 和 $v$，满足：

$$\parallel f(u)-f(v){\parallel }_{\mathrm{\infty }}\le \gamma \parallel u-v{\parallel }_{\mathrm{\infty }}$$

详细证明略

‍

由此，我们可知解存在，并可以采用迭代方法求解：只需要随机初始化一个 $v_0$，不断应用函数 $v_{k+1}=f(v_k)$，足够多步后我们能够得到最优的 $v^{\ast }$